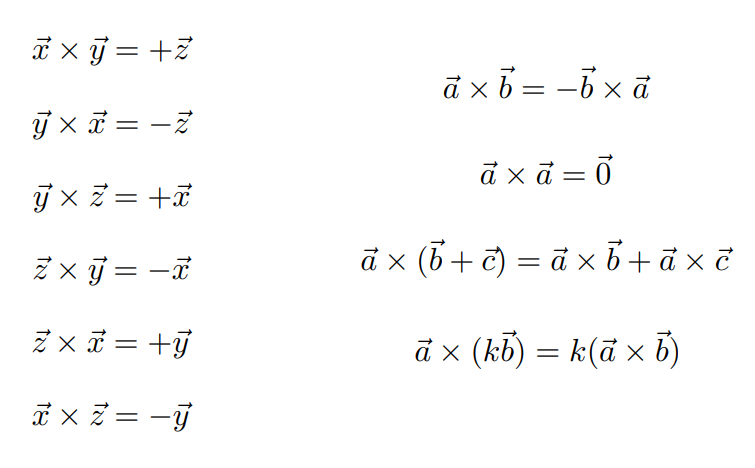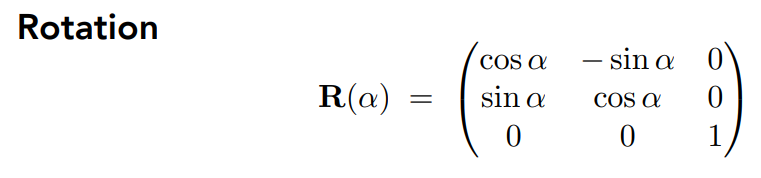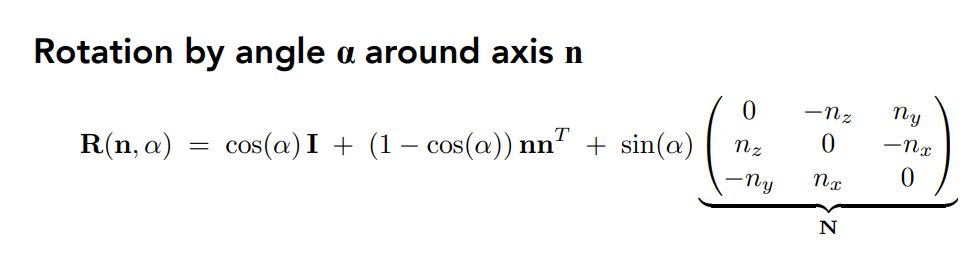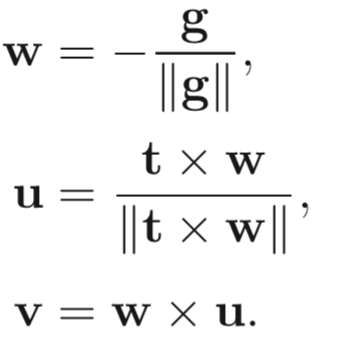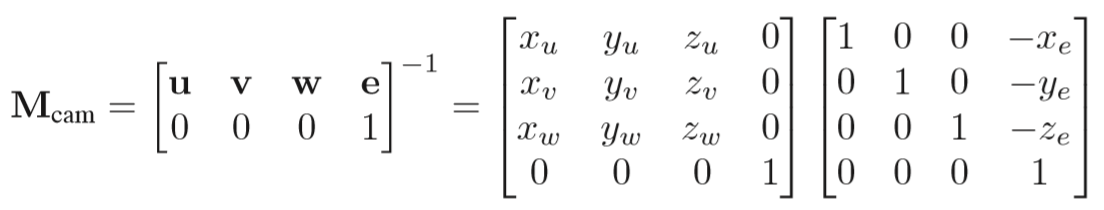Overview
画面好不好的简单标准:是否足够亮(渲染中的关键技术:全局光照)
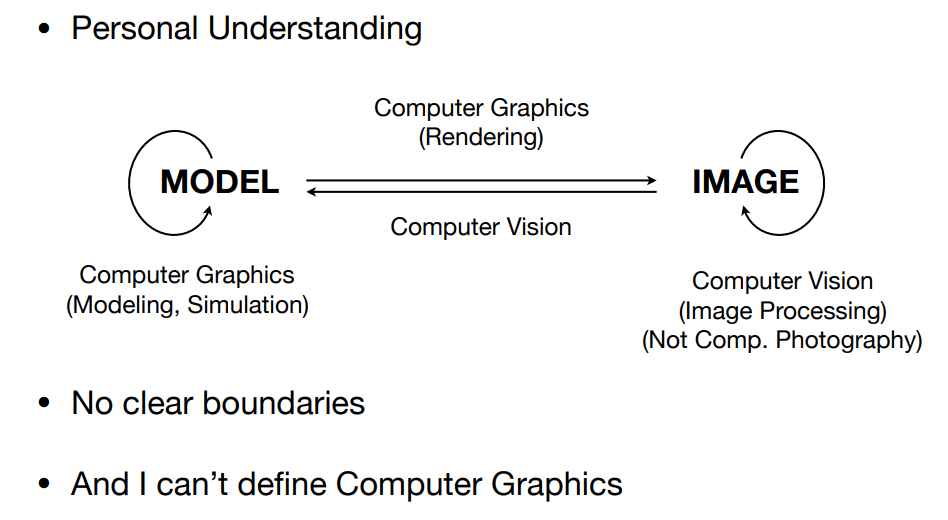
计算机图形学和计算机视觉的区别(计算机图形学做的事是什么):
计算机视觉包括猜测
渲染的具体定义:https://www.zhihu.com/question/31971846
A Swift and Brutal Introduction to Linear Algebra!
Dot Product in Graphics
- Find angle between two vectors
- Finding projection of one vector on another
- Measure how close two directions are (Projection)
- Decompose a vector (Projection)
- Determine forward / backward ( dot product > or < 0 )
Cross product
Properties
In Graphics
- Determine left / right
- Determine inside / outside (三角形内部外部)
corner case: 随意
Matrix-Matirx Multiplication
x行y列,对应原来两个矩阵 x行行向量 和 y列向量 点乘的值
叉乘和矩阵乘法不满足交换律
Transformation
Homogeneous Coordinates
2D point = (x, y, 1)^T
2D vector = (x, y, 0)^T *向量具有平移不变性,这个可以使得向量(x, y, 0)经过平移变换后,仍是(x, y, 0)
- vector + vector = vector
- point – point = vector
- point + vector = point *点沿着一个向量移动到另一个点上
- point + point = ?? *点+点 = 中点(将每个元素除以w = 2)
*仿射变换的最后一行都是000…01,投影变换不是
Linear map
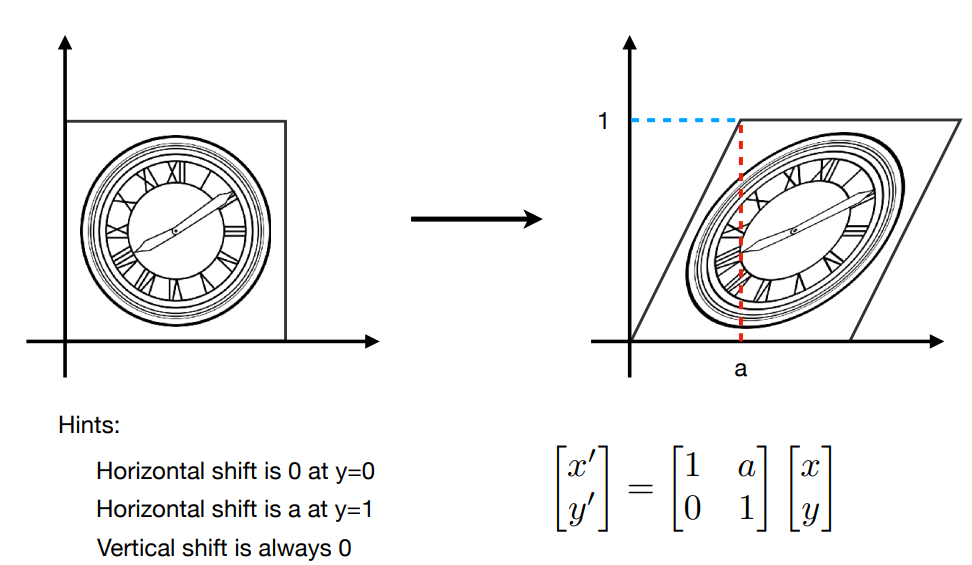
Shear Matrix
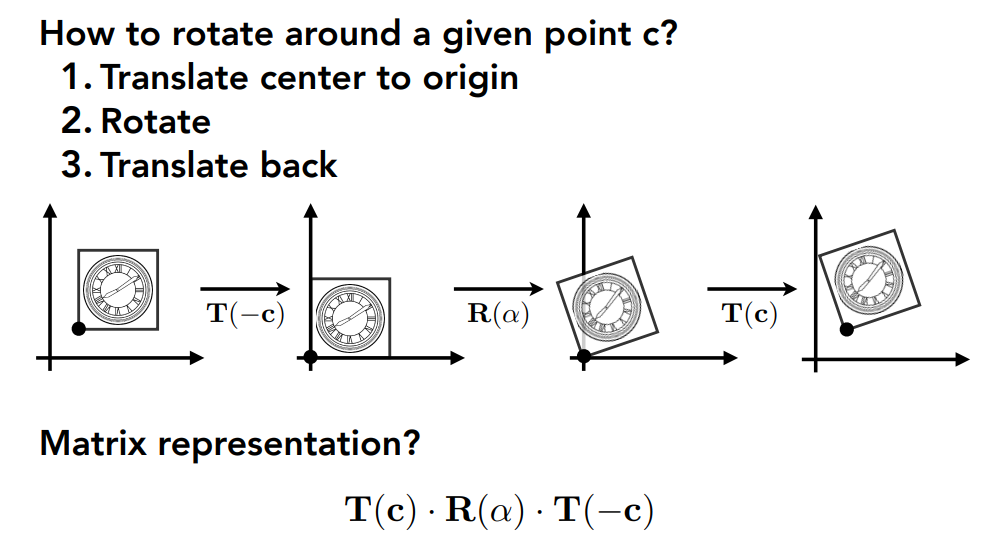
Rotate
默认:逆时针绕原点旋转
旋转-θ角,R(-θ) = R(θ)的转置 = 逆操作 (正交矩阵)
Affine map
Inverse Transform
变换的顺序很重要!(先旋转还是先平移?)
变换矩阵从右乘到左
Decomposing Complex Transforms
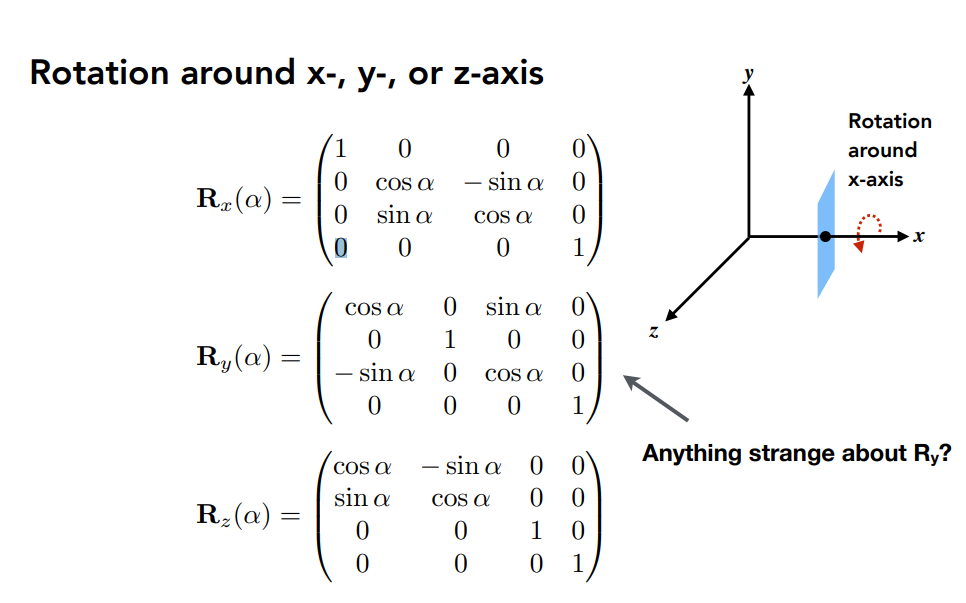
3D Transforms
先应用线性变换再平移
Rotations
Rodrigues’ Rotation Formula
欧拉角和四元数
老师说四元数适合做差值
Viewing transformation
View / Camera Transformation
We always transform the camera to
- The origin, up at Y, look at -Z
- And transform the objects along with the camera
具体操作
我们定义:
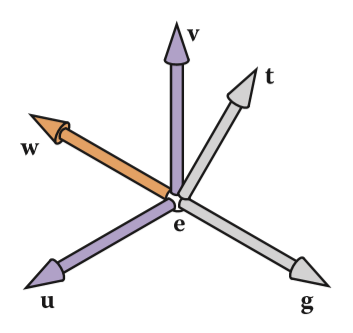
相机或眼睛位置 (eye postion) e
观察方向 (gaze postion) g
视点正上方向 (view-up vector ) t
建立摄像机坐标系:
如此成功建立摄像机坐标系之后,如何将其移动到原世界坐标系呢?
- 将相机位置移动至原点
- 通过旋转矩阵将二者坐标系重合
第一步只需简单的减去相机位置坐标 e 即可,而第二步也只需用( u , v , w ) T 矩阵便可轻松表示将摄像机坐标系旋转至世界坐标系了
M = R·T *因为要先平移再线性变换,所以R和T要分开写
老师的写法:
*Also known as Model/View Transformation