Sample
计算机生成图像时,最基本的多边形是三角形,对三角形的离散化就是生成图像的重点。那么如何离散化(光栅化)?采样!一个像素点对应一个坐标点,对这个坐标点采样,判断它在不在三角形里面。
所以采样的缺点是:以点代面,有失偏颇 -> Aliasing走样,表现为锯齿
Photograph = Sample Image Sensor Plane
Video = Sample Time
Artifacts: Aliasing
- Jaggies
- Moiré Patterns(不太懂原理,看别人的笔记后面第八节课好像会讲)
- Wagon Wheel Illusion (False Motion):视觉上倒转
Behind the Aliasing Artifacts
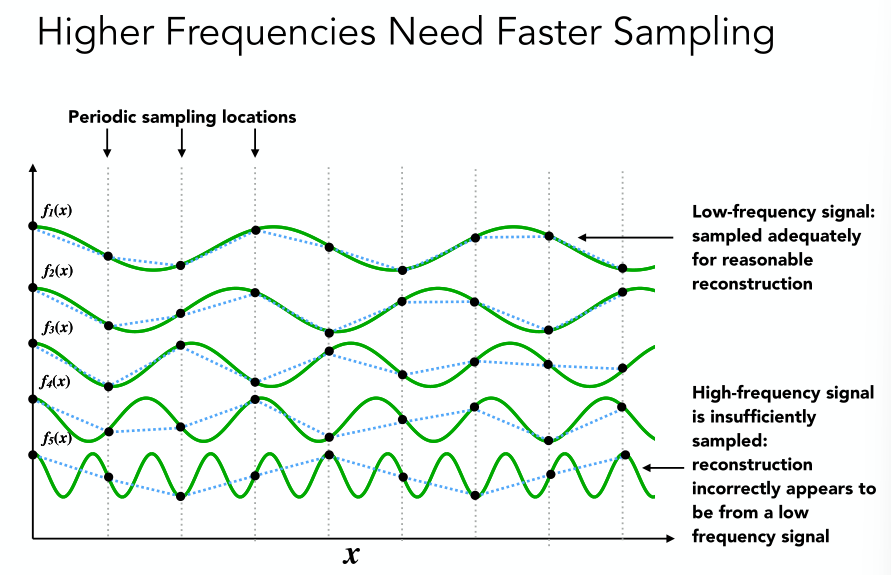
- Signals are changing too fast (high frequency), but sampled too slowly
Antialiasing Idea
Blurring (Pre-Filtering) Before Sampling
不可以反过来,反过来叫Blurred Aliasing
下面开始讲原理部分
Frequency Domain
Frequencies
cos2Πfx 频率为f,周期为T=1/f
傅里叶级数展开
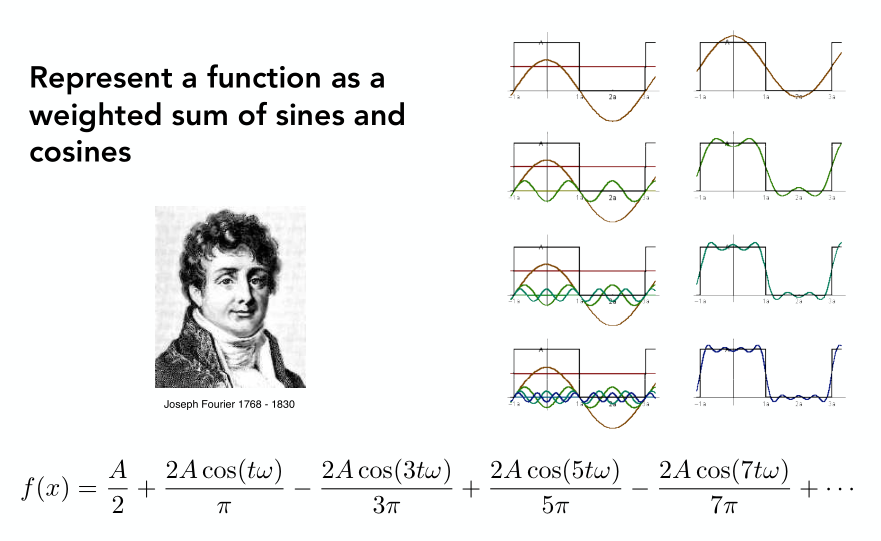
Represent a function as a weighted sum of sines and cosines
傅里叶级数展开,可以将任一函数表示为余弦线性组合+常量
傅里叶变换
Fourier Transform Decomposes A Signal Into Frequencies
傅里叶变换和逆变换,实现了时域函数和频域函数的转换。
时域: 是真实世界,是惟一实际存在的域。可以这样理解,从我们出生开始,所接触的这个世界就是随着时间在变化的,是在运动的。
频域:频域它不是真实的,而是一个数学构造。结合上面对时域的理解,如果时域是运动永不停止的,那么频域就是静止的。
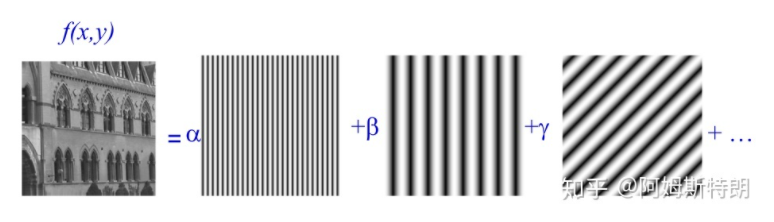
所以任何函数可以分解为不同的频率(从低到高)
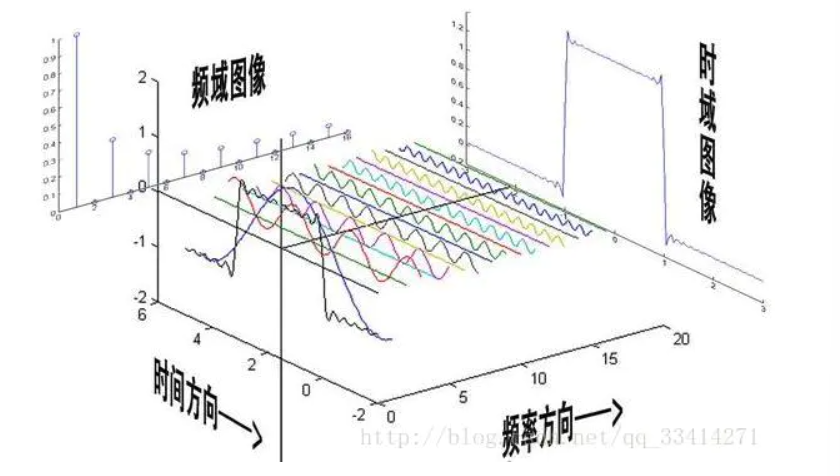
在频域中,函数变成不同频率的段并显示
从时域来看,我们会看到一个近似为矩形的波,而我们知道这个矩形的波可以被差分为一些正弦波的叠加。
而从频域方向来看,我们就看到了每一个正弦波的幅值,可以发现,在频谱中,偶数项的振幅都是0,也就对应了图中的彩色直线、振幅为 0 的正弦波。
Filtering = Getting rid of certain frequency contents
傅里叶变换可以把一个函数从时域变成频域。
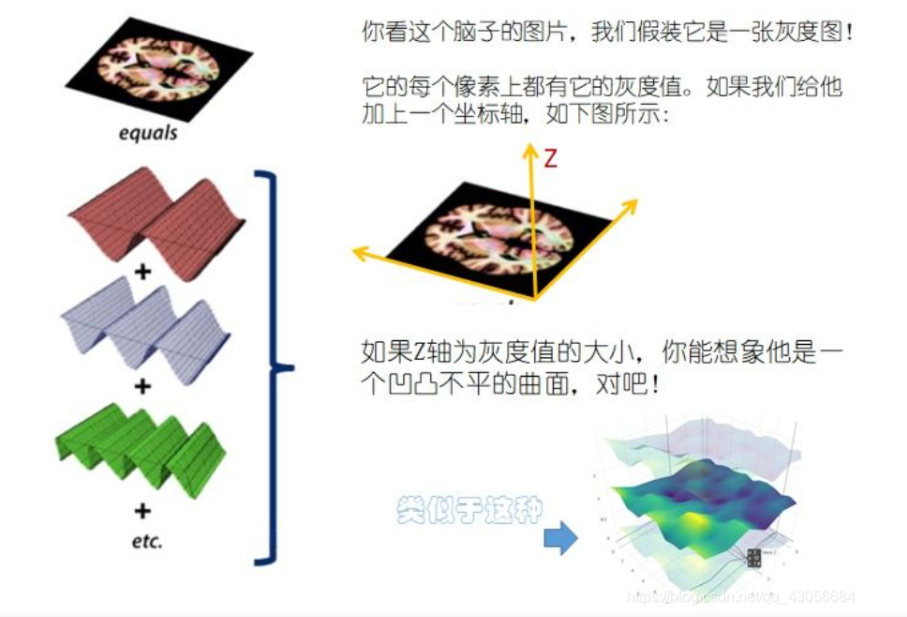
图像和波
参考 https://www.ruanyifeng.com/blog/2017/12/image-and-wave-filters.html
如果把每一行所有像素的红、绿、蓝的值,依次画成三条曲线,就可以得到图像波。
有些区域的波动比较小,有些区域突然出现了大幅波动。
对比一下图像就能发现,曲线波动较大的地方,也是图像出现突变的地方。
综上所述,图像就是色彩的波动:波动大,就是色彩急剧变化;波动小,就是色彩平滑过渡。因此,波的各种指标可以用来描述图像。
- 色彩剧烈变化的地方,就是图像的高频区域;色彩稳定平滑的地方,就是低频区域。
图像不过是个二维数组,方便理解起见,咱们可以考虑一维数组
下面的例子可能不严谨,但绝对很直观
比如有如下数组
{1, 10, 1, 10, 1, 10, 1, 10, 1, 10, 1, 10}
和
{1, 2, 3, 4, 5, 4, 3, 2, 1, 2, 3, 4, 5, 4, 3, 2, 1,}
你直观的理解下,哪个数组的”频率”大点?
你可以用纵坐标代表数组值,横坐标代表数组index描点看看,显然是第一个数组的频率高。
所以对于数组来说,数字之间变化剧烈,代表高频,柔和代表低频。同理,对于图像来说,那就是灰度变化快的是高频,慢的是低频。比如一个物体的边缘,就是高频信号,物体内部就是低频。
二维傅里叶变换
一个二维函数可以使用无数个x方向的正余弦函数与y方向的正余弦函数的乘积形式表示, 是乘积的叠加,它的正变换表示当x方向的频率为u、y方向的频率为v时对应的二维正余弦函数的幅值,总共有四种组合:sinux·sinvy, sinux·cosvy, cosux·sinvy, cosux·sinvy。
一维的频谱横坐标就是频率,f(x)= y的意思就是图像上的x频率有y这么多。
二维没有所谓横坐标概念,他是u和v两个坐标轴。f(u,v)= y的意思就是(u,v)这个频率的大小为y。
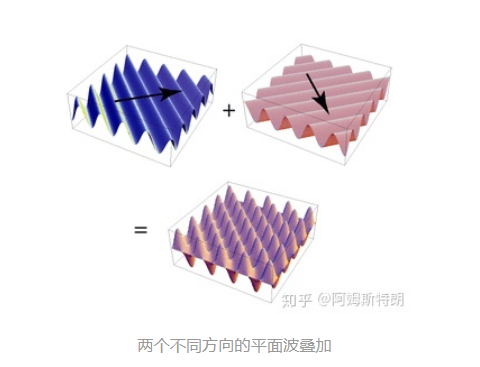
那(u,v)又是个啥频率呢?你可以想象下,一个二维的丘陵地区(二维图像),你沿不同方向看,它的频率可以不一样。比如沿着山脊走,就很平坦,频率很低,但垂直山脊走那就是直接跳崖,频率很高。所以你想表示频率,得至少用到两个变量–比如(100,10)就表示横向看频率为100,但纵向看频率只有10的频率。也就是一副纵向走向的山脊的图形。所以二维图像傅里叶可以让你看到各个方向上频率的多少
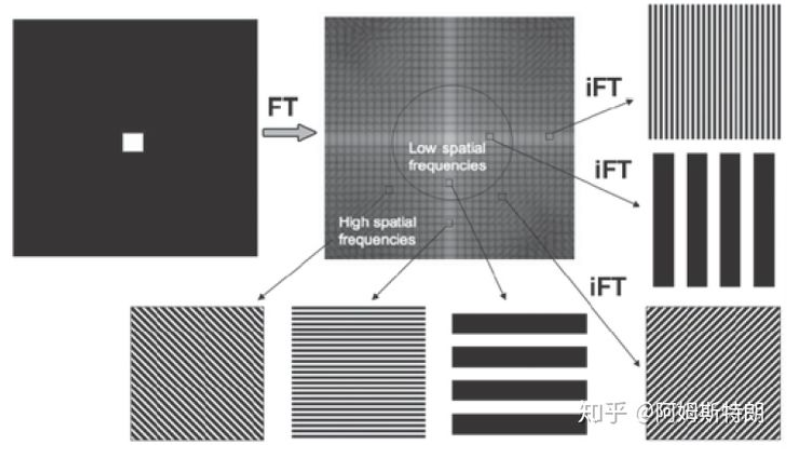
二维频谱图
与一维信号类似,二维图片也可以用多种不同方向和频谱的正弦图叠加表示。 一张正弦图片可以由一对频谱点表示,频谱点距离表示频率,角度表示正弦图片的角度。
1. 空间域:
空间域(spatial domain)也叫空域,即所说的像素域,在空域的处理就是在像素级的处理,如在像素级的图像叠加。通过傅立叶变换后,得到的是图像的频谱,表示图像的能量梯度。2. 时域:
时域(时间域)——自变量是时间,即横轴是时间,纵轴是信号的变化。其动态信号x(t)是描述信号在不同时刻取值的函数。
性质
- 中心最低频,贡献了图像的主体,信息量多
- 周围高频提供图像的细节和边缘,信息量少,边缘就是图像信息变化剧的部分
高通滤波&低通滤波
高通滤波:只有高频信号可以通过,只留下低频信息,得到模糊的图
低通滤波:只有低频信号可以通过(水波纹 不完美的低通滤波 说后面会再提)
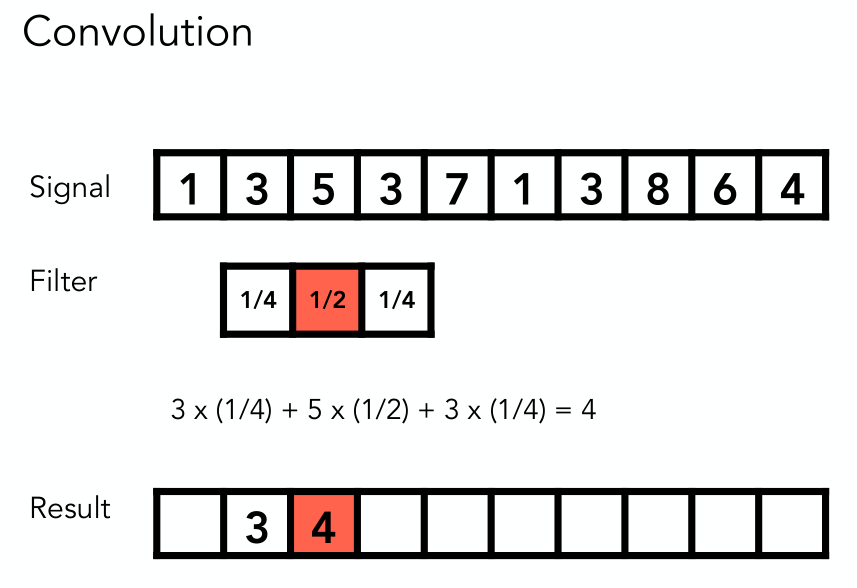
Filtering = Convolution (= Averaging)
图形学上的简易卷积
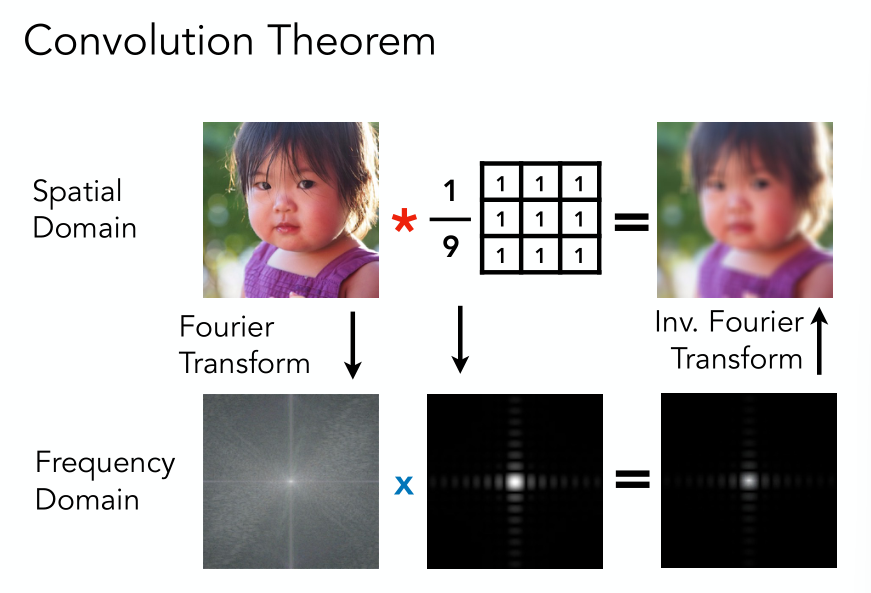
Convolution Theorem
Convolution in the spatial domain is equal to multiplication in the frequency domain, and vice versa
时域卷积定理 即时域内的卷积对应频域内的乘积;
频域卷积定理 即频域内的卷积对应时域内的乘积
选择1:
- 滤波器对图做卷积操作
Filter by convolution in the spatial domain
选择2:
- Transform to frequency domain (Fourier transform)
- Multiply by Fourier transform of convolution kernel
- Transform back to spatial domain (inverse Fourier)
- 图先傅里叶变换到频域上
- 卷积的滤波器变到频域上
- 两者相乘得到频域的结果
- 逆傅里叶变换变到时域上
回到采样
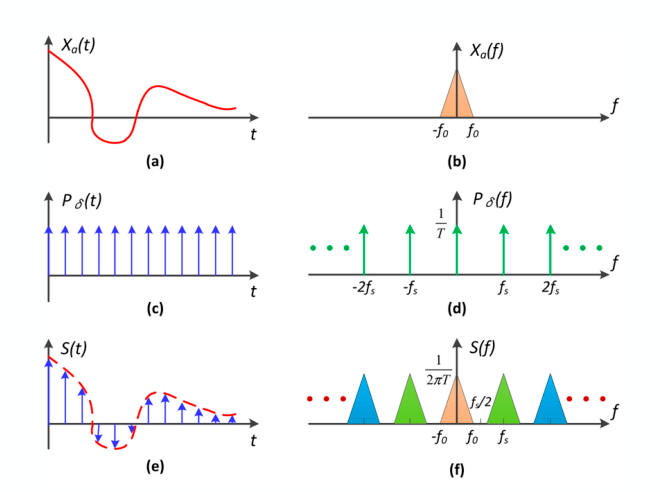
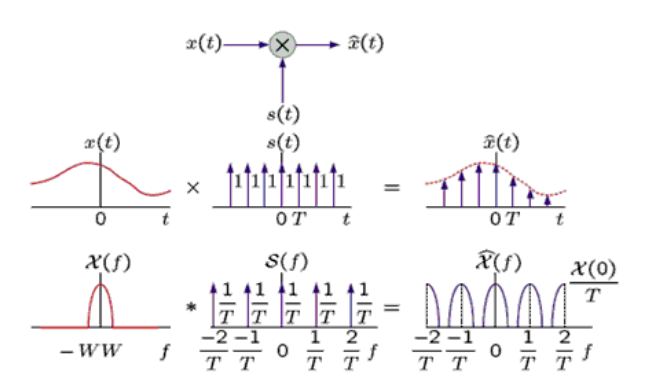
Sampling = Repeating Frequency Contents
a*c 得到采样结果(a中函数的瞬时值)(时域的乘积),可以看到采样结果的频谱(频域的卷积)是复制粘贴频谱
所以采样的频谱实际上就是在重复原始信号频谱
卷积的重要的物理意义是:一个函数(如:单位响应)在另一个函数(如:输入信号)上的加权叠加。
重复一遍,这就是卷积的意义:加权叠加。
具体见:https://blog.csdn.net/bitcarmanlee/article/details/54729807
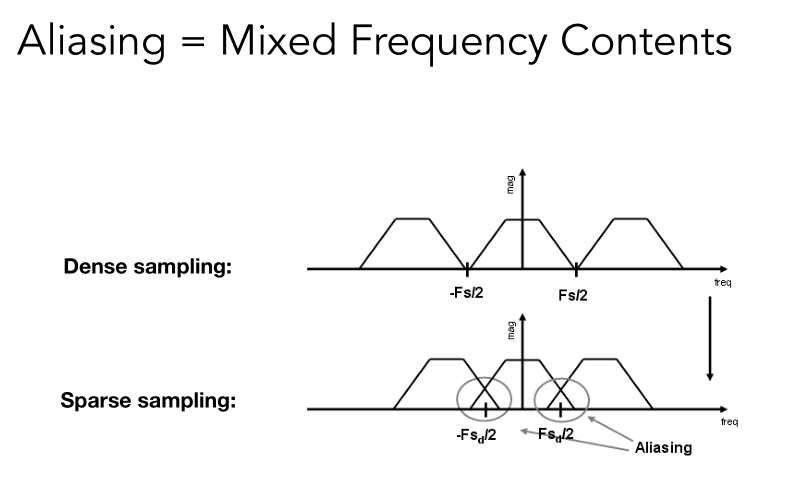
Aliasing = Mixed Frequency Contents
采样越稀疏,频谱的搬移越密集
走样原因:频谱混合
How Can We Reduce Aliasing Error?
Increase sampling rate
- Essentially increasing the distance between replicas in the
Fourier domain - Higher resolution displays, sensors, framebuffers…
- But: costly & may need very high resolution
- Essentially increasing the distance between replicas in the
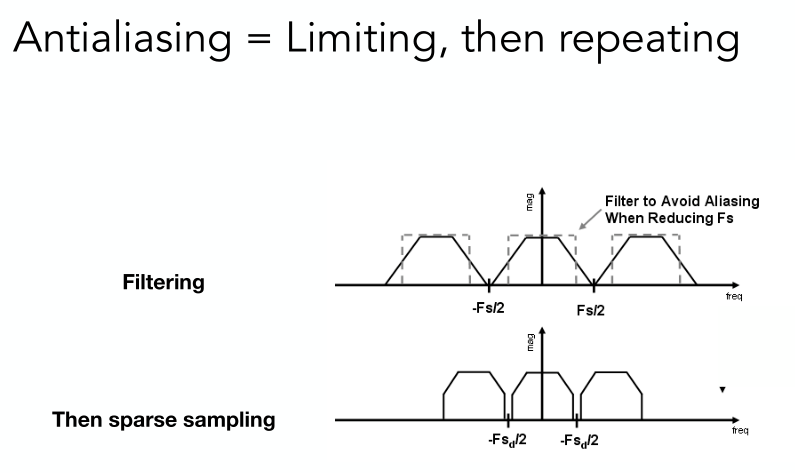
Antialiasing
- Making Fourier contents “narrower” before repeating
- i.e. Filtering out high frequencies before sampling 采样前用一定大小的低通滤波器卷积
为什么先采样再模糊不行:因为这样做等于先把信号混叠再截断信号,混叠的信号还是混叠的
Antialiasing By Averaging Values in Pixel Area
Solution: 一个像素内部的值在覆盖面积上求平均
- Convolve f(x,y) by a 1-pixel box-blur
-Recall: convolving = filtering = averaging - Then sample at every pixel’s center
In rasterizing one triangle, the average value inside a pixel area of f(x,y) = inside(triangle,x,y) is equal to the area of the pixel covered by the triangle.
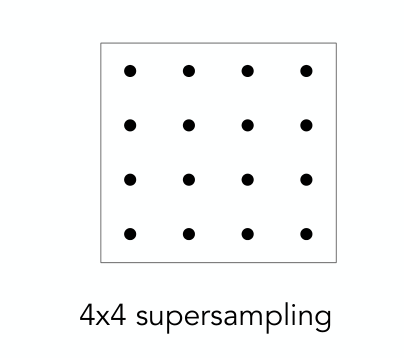
Antialiasing By Supersampling (MSAA)
Supersampling
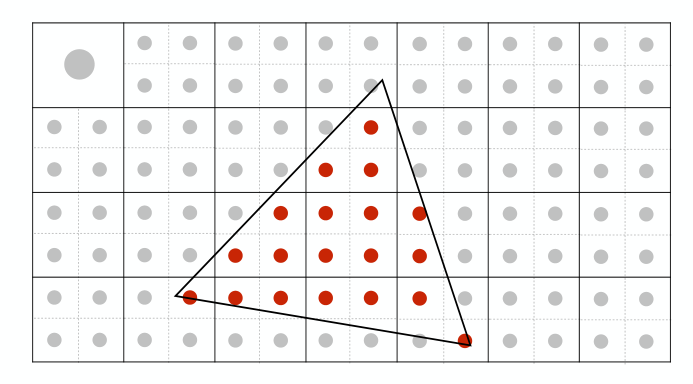
认为一个像素被划分为好多个带中心的小像素,是对覆盖区域的近似
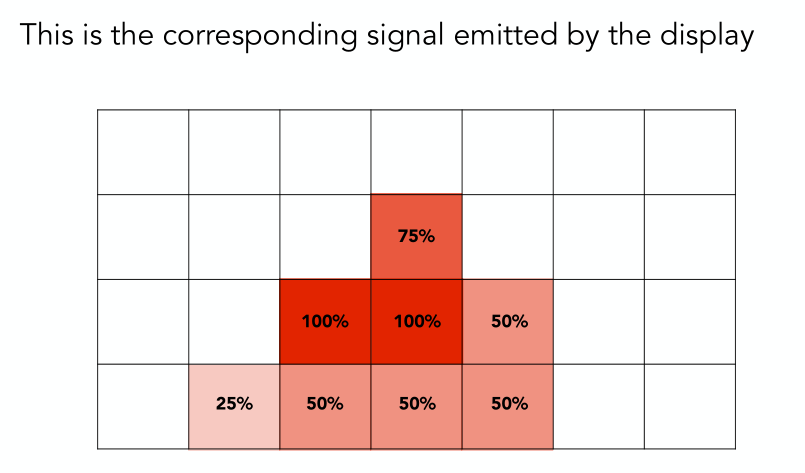
比如2x2的supersampling 一个小像素覆盖25% 三个小像素75%
解决的是模糊的操作,没有提高采样率
cost of MSAA
- 增大计算量
- 工业界实际:样本复用、不规则分布等
Antialiasing Today
Milestones
FXAA 快速近似抗锯齿
找到锯齿边界,换成没有锯齿的边界(而且速度很快)
TAA 简单 高效
找上一帧的信息 复用上一帧的结果 相当于MSAA 对应的样本分布在时间上(静态的)(没太懂)
查了一下大概是:在每帧采样时,将采样的点进行偏移,实现抖动 (jitter)。 当场景静止时,因为每一帧的投影矩阵都被微小偏移,所以我们可以直接混合某一点前几帧的值来实现抗锯齿。
Super resolution / super sampling
- 超分辨率 From low resolution to high resolution:把一张低分辨率的图拉大
- Essentially still “not enough samples” problem
- DLSS 深度学习 细节缺失->深度学习猜