从4开始的图形学入门生活（Z-buffer & Lambertian (Diffuse) Shading）

课程链接：https://www.bilibili.com/video/BV1X7411F744?from=search&seid=944040088923830300&spm_id_from=333.337.0.0

课程PPT：https://sites.cs.ucsb.edu/~lingqi/teaching/games101.html

作业链接：http://games-cn.org/forums/topic/allhw/

Z-buffer 深度缓存

之前解决的是一个三角形光栅化的问题，现在要考虑多个三角形光栅化覆盖的问题

Painter’s Algorithm

（油）画家算法：由远及近画画，覆盖

• 需要对深度进行计算与排序
• 有n个三角形时，时间复杂度O(nlogn)
• 可能有无法排序的情况：例如三个三角形互相重叠

Z-buffer

Idea

• Store current min. z-value for each sample (pixel)
• Needs an additional buffer for depth values
  • frame buffer stores color values
  • depth buffer (z-buffer) stores depth

For simplicity we suppose z is always positive

i.e. (smaller z -> closer, larger z -> futher)

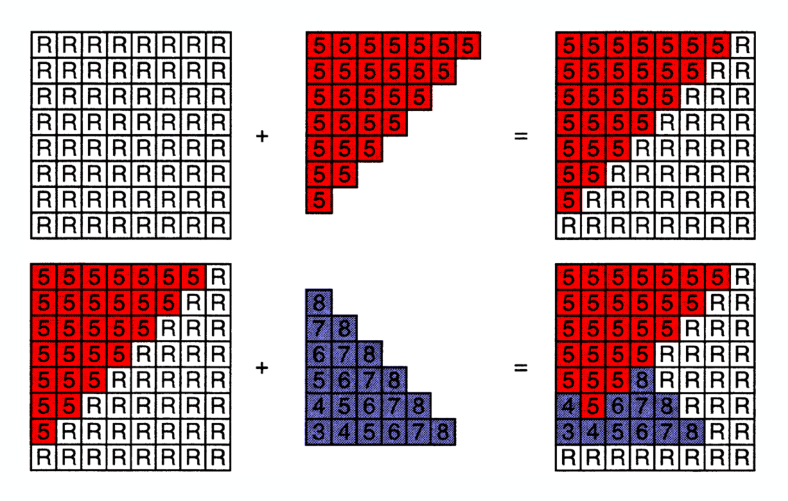
Example

把深度值转化为颜色值，近小远大，所以近处的是黑的，远处的是白的。

Algorithm

c++

Initialize depth buffer to ∞ 
During rasterization: 

	for (each triangle T)
		for (each sample (x,y,z) in T)
			if (z < zbuffer[x,y])			// closest sample so far
				framebuffer[x,y] = rgb;		// update color
				zbuffer[x,y] = z;       	// update depth
			else
				; 			// do nothing, this sample is occluded

Complexity

• O(n) for n triangles（考虑每个三角形覆盖常数个像素）

  不是排序算法，而是求最小值

• 基本上不会有两个完全相同深度的像素（浮点数不能精确的表示有理数）

  假设没有相同深度的两个像素，深度缓存和画三角形的顺序无关

• Most important visibility algorithm : Implemented in hardware for all GPUs

• 无法处理透明物体

Shading

Definition

• In Merriam-Webster Dictionary

  • shad·ing, [ˈʃeɪdɪŋ], noun
    The darkening or coloring of an illustration or diagram with parallel lines or a block of color.

• In this course

  • The process of applying a material to an object.

    不同的材质和光线有不同的相互作用的方法

Perceptual Observations

如图所示，可以将光线简单地分为三类：

1. 镜面高光
2. 漫反射
3. 环境光

In this course，

• 光强，光的亮度，光的能量皆指同一个概念，目前阶段暂不做区分
• 所有方向向量都为单位向量

Shading is Local (局部)

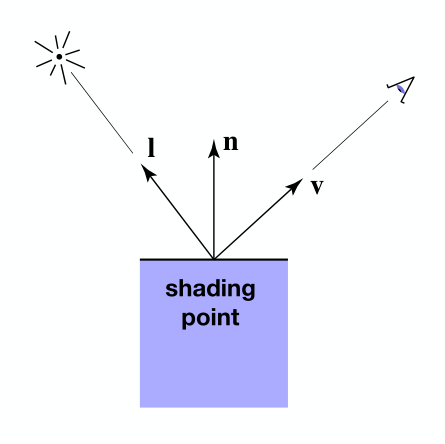
• Compute light reflected toward camera at a specific shading point

• Inputs：

  • Viewer direction, v

  • Surface normal, n 平面法向量

  • Light direction, l

    (for each of many lights)

  • Surface parameters
    (color, shininess, …)

• No shadows will be generated! (shading ≠ shadow)

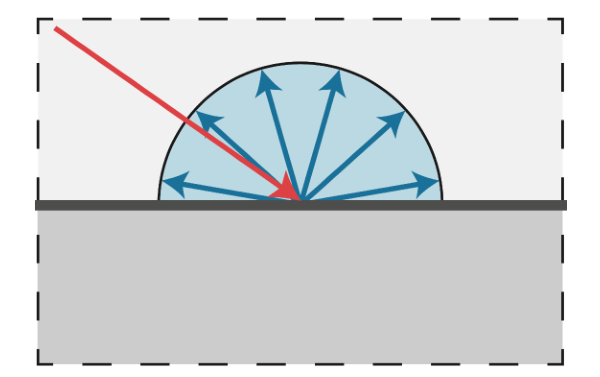
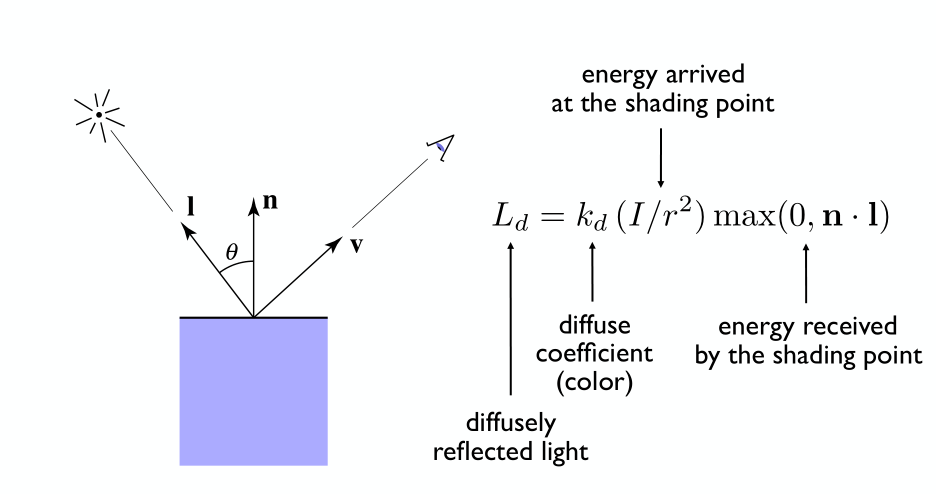
Diffuse Reflection

• Light is scattered uniformly in all directions
  • Surface color is the same for all viewing directions

Lambertian (Diffuse) Shading

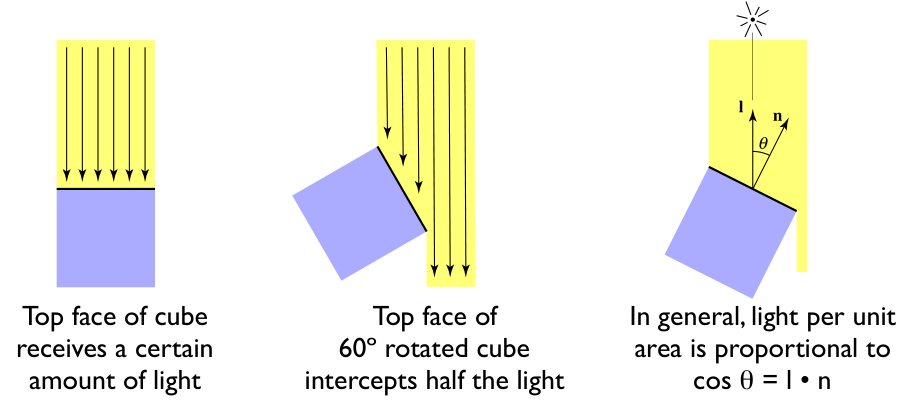
Lambert’s cosine law: how much light (energy) is received?

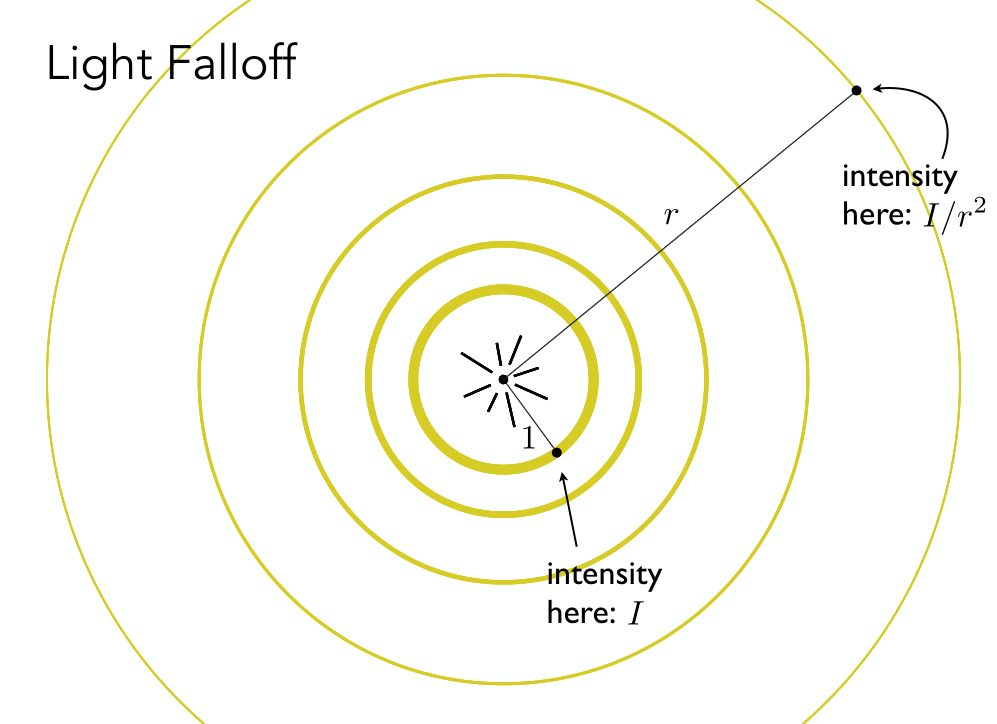
Light Falloff

想象一个逐渐扩散变大的球壳

Lambertian (Diffuse) Shading

Shading independent of view direction